In an attempt to make the subject easier for people to understand, a programmer ran MITTENS through ChatGPT, and despite the usual issues and very generous assumptions of tiny populations and high fixation probabilities, the results tend to demonstrate why biologists will have to avoid MITTENS as long as they possibly can in order to continue clinging to their outdated and disproven assumptions about the origin of the species. Somewhat amusingly, the AI did not provide a final answer in terms of the range of times required for fixation given its estimates and assumptions, but contented itself with saying that a population-wide fixation could perhaps happen eventually, in theory, given a sufficiently beneficial mutation.
This AI-generated summary usefully points the way toward filling in the various blanks that would permit a full fixation simulator to provide valid answers when prompted with the relevant variables that can be derived from existing genetic studies, such as observed selection coefficients and drift factors. Interestingly enough, even the analogy of the simplified explanation demonstrates the implausibility of the fixations required for every human to possess the same human-specific genes sans a mechanism far more akin to IGM than TE(p)NSBMGDaGF.
As it turns out, the AI is effectively “smarter” than the biologists, because unlike biologists like JFG and Richard Dawkins, the AI “comprehends” that the mathematical challenges posed are both relevant and real.
Simplified Explanation for Non-Mathematicians
Think of mutation and fixation in genetics akin to introducing a new smartphone model and observing how quickly it becomes the only model used by everyone. Mutation rate is like the frequency of new model launches, while fixation rate is like observing how quickly each new model becomes the dominant one used by the public. Selective events are like market conditions that favor the rapid adoption of certain models over others (e.g., a significant technological advancement).
Understanding Fixation Rate with an Example
The fixation rate in a population genetics context refers to the frequency at which a particular mutation becomes present in every individual of a population, effectively replacing all other versions of that gene. Let’s break down the concept of fixation rate using a simplified example.
Example: Introducing a Beneficial Mutation in a Small Population
Imagine a small population of 1000 butterflies. A mutation occurs in one butterfly that makes its wings brighter, potentially giving it a better chance of avoiding predators.
Step 1: Mutation Occurs
- Initial mutation: One butterfly develops a mutation for brighter wings.
- Population size (N): 1000 butterflies.
- Number of mutants at the start (m): 1.
Step 2: Determine Fixation Probability
For a beneficial mutation, the fixation probability can be higher than that of a neutral mutation. If we assume this mutation offers a slight survival advantage, let’s denote the selection coefficient by 𝑠s, where 𝑠s is small, say 0.01 (1%).
The fixation probability (𝑃P) for beneficial mutations can be approximated using the formula:
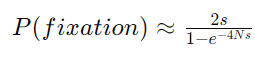
𝑃(𝑓𝑖𝑥𝑎𝑡𝑖𝑜𝑛)≈2𝑠1−𝑒−4𝑁𝑠P(fixation)≈1−e−4Ns2s
Plugging in our numbers:
- 𝑁=1000 (population size),
- 𝑠=0.01 (selection advantage).
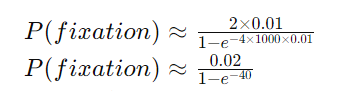
𝑃(𝑓𝑖𝑥𝑎𝑡𝑖𝑜𝑛)≈2×0.011−𝑒−4×1000×0.01P(fixation)≈1−e−4×1000×0.012×0.01 𝑃(𝑓𝑖𝑥𝑎𝑡𝑖𝑜𝑛)≈0.021−𝑒−40P(fixation)≈1−e−400.02
Since 𝑒−40e−40 is a very small number close to zero, the formula simplifies to:
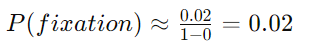
Step 3: Calculate the Fixation Rate
The fixation rate involves how quickly this mutation spreads through the entire population until it becomes the only variant present. This rate not only depends on the fixation probability but also on factors like the generation time and population dynamics. If the mutation indeed confers a survival advantage, and given that the probability of fixation is about 2%, it implies that in favorable conditions, it might eventually spread to the entire population.
Step 4: Observing the Outcome
- Generational time: Assuming each butterfly generation spans one year.
- Over many generations, we observe whether the mutation spreads and reaches fixation (where all 1000 butterflies have the mutation) or is lost due to drift or other factors.
Key Takeaways
- Fixation Probability: Even with a beneficial mutation, the probability of fixation isn’t guaranteed but is significantly higher than for neutral mutations. In our example, there’s a 2% chance the beneficial mutation will fixate in the population.
- Impact of Population Size: Larger populations may see a slower spread of mutations due to their sheer size and genetic diversity.
- Role of Selection Coefficient: A higher 𝑠s value (greater advantage conferred by the mutation) increases the probability of fixation.